Visual Logic: A New Book by Fr. John Rickert
Fr. John P. Rickert, FSSP published a new book in August called Visual Logic: Seeing Classical and Modern Logic, An Introduction. He graciously agreed to answer a few questions on the book and address topics that may be of interest to our readers. –ed.
Q: Why is logic an important subject for Catholics, even those of us who don’t have a career in philosophy or mathematics?
A: Logic, at least to some extent, is necessary for meaningful communication. We have to understand correctly what is being asserted and what is not being asserted, and we have to see whether truths are connected, and if so, how.
 Q: In the book you decry the separation of classical and modern logic. Our FSSP readers probably need no convincing of the former’s value! So what, in your view, have modern theorists brought to the table that has advanced the subject?
Q: In the book you decry the separation of classical and modern logic. Our FSSP readers probably need no convincing of the former’s value! So what, in your view, have modern theorists brought to the table that has advanced the subject?
A: The most important contribution of Modern Logic, in my opinion, was the discovery that logic itself has limits; logic proves that there are true statements that cannot be proved. As the saying goes, “Truth is greater than proof.” In my view, this truth is so important that every educated adult should be aware of it. Modern Logic has also developed in various directions, such as Modal Logic, that the ancients had only glimpses of.
Q: You mention how Kurt Gödel showed the limitations of arithmetic in the 1930s, in contrast with David Hilbert who didn’t seem to admit any such limitation. Is there a wider lesson here about human knowledge that you are pointing to?
A: Yes. The fact that science relies so heavily on mathematics will mean that, at least in theory, there are questions that science will never be able to answer. “Theories of Everything” are an exaggeration, considering that only about 4% of matter is understood and 96% remains a mystery. But even aside from these percentages, there is the more fundamental point that science doesn’t have all the answers. Indeed, science doesn’t even have all the questions.
Q: Logic seems like a very abstract thing to study. But you point out that real-world electronics and computers depend on it. How?
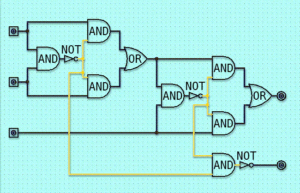 A: Computers, cell phones, and practically anything programmable such as microwaves use “logic gates” that implement logical ideas such as “and,” “or,” “not,” and “if.” The logical framework they use is due to George Boole and is also a great triumph of Modern Logic. In a way it is remarkable that people can use these inventions without having to know the underlying logic, but it is intellectually rewarding to have some idea of what is going on deep down.
A: Computers, cell phones, and practically anything programmable such as microwaves use “logic gates” that implement logical ideas such as “and,” “or,” “not,” and “if.” The logical framework they use is due to George Boole and is also a great triumph of Modern Logic. In a way it is remarkable that people can use these inventions without having to know the underlying logic, but it is intellectually rewarding to have some idea of what is going on deep down.
Q: You spend several pages on the meaning of the word “if”, and it ends up in a pretty weird place!
A: It does! I think this is an example of why I say that logic straddles both mathematics and philosophy; it does not fit exclusively into either one of these. Ultimately, for logicians, “if” becomes a technical term, like the terms “and,” “or,” and “not,” and then one proceeds on the basis of the definition. Still, this convention does leave a significant gap between what a mathematician or logician means by the word and what all of us in everyday life mean by it, and there are some weird results.
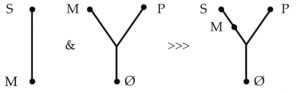
Q: How do visual representations, like the I-graph system or Venn diagrams, help us understand logic?
A: It is a commonplace among mathematicians that most people are either more “computational” (algebraic) or “geometric” (visual) in how they like to understand things. Of course, some are highly gifted at both ways of understanding something. Modern Logic is very heavily algebraic in its approach. There are good reasons for this: For one thing, one can check a proof as mechanically as one can check a calculation. Still, the intuitive side of logic can easily be lost in this approach.
A long time ago, when I studied logic for the first time, I read a very classical treatment that used the system of moods and figures. I am not sure whether I really “got” it, to be honest, but the thought lingered with me for a long time that there must be a clean, simple, easy way to see logic so that it is obvious, and not just the application of memorized rules.
All of sudden, in 2018, it hit me how to represent statements visually, and that combining the diagrams would visualize a syllogism. I have not seen this treatment elsewhere, so a major reason why I wrote the book was to present this approach. I must give my guardian angel a lot of credit. In fact, some very helpful insights came to me even in the course of writing the book.
Q: Who do you think would benefit most from this book?
A: My hope is, if this is not too ambitious, those who are perhaps curious about logic but find it too off-putting, or those who have felt somewhat frustrated by what they have seen of it before. I would be delighted if others experience the sort of “Eureka!” that I did.
Visual Logic: Seeing Classical and Modern Logic is available at Amazon.com.
December 2, 2022